A zero-knowledge proof is a method of proving you know something or have certain information without actually sharing that information.
Example: The Two Doors Cave 1
Imagine there’s a cave with only one entrance. Inside, there’s a magic door that separates two paths. Your friend claims they know the secret phrase to open the magic door. How can they prove it to you without revealing the phrase?
- The Proof: You stand outside the cave entrance. Your friend goes into the cave and randomly chooses one of the two paths. Then, you shout out the name of one of the paths (you choose randomly!). Your friend comes back out of the cave through the path you named.
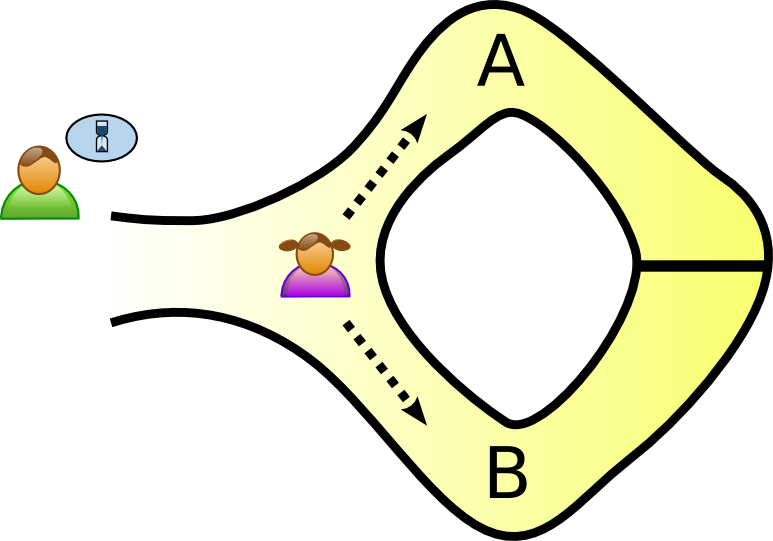
- Why it works: If your friend truly knows the secret phrase, they can always open the magic door and return through the path you call out. If they were just guessing, there’s a 50% chance they’d come out the wrong way. If you repeat this process many times, you’ll become very confident that they indeed know the secret phrase.
The three key properties of a zero-knowledge proof are:
- Completeness: If the statement is true, it’s possible to convince the verifier.
- Soundness: If the statement is false, it’s impossible to trick the verifier.
- Zero-knowledge: The verifier learns nothing beyond the validity of the statement.
Zero-knowledge proofs are used in cryptography to authenticate users, verify identities securely, and protect privacy by ensuring authentication doesn’t require sharing sensitive information like passwords or credentials.
Footnotes
-
This is simplified from How to Explain Zero-Knowledge Protocols to Your Children by Jean-Jacques Quisquater and other in Advances in Cryptology — CRYPTO’ 89 Proceedings ↩